Contoh Soal Diagonal Ruang Kubus dan Diagonal Bidang (SISI) serta Contoh soal - Caraguha

Secara umum diagonal adalah garis yang mengubungkan antara satu sudut dengan sudut lainnya yang bersebrangan sehingga selalu melintang. 

Seperti yang kita ketahui bahwa kubus merupakan bangun ruang sehingga memiliki diagonal ruang dan diagonal bidang (diagonal sisi)

jika kita imajinasikan, Jaring-jaring kubus terbentuk oleh bangun datar persegi sehingga diagonal sisi (bidang) itu merupakan garis yang membentang dari sudut ke sudut persegi (bersebrangan)

sedangkan diagonal ruang adalah garis yang yang melewati titik tengah kubus atau garis yang melalui ruang. biar gak bingung langsung saja kita lihat gambar

dan Berikut merupakan gambar kubus. untuk mengetahui perbedaan diagonal ruang dan diagonal bidang (diagonal sisi) mari lihat pernjelasan dibawah ini

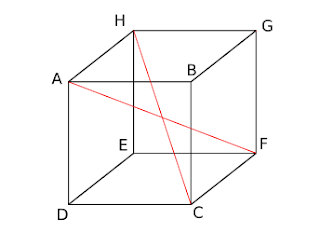
Dari gambar diatas yang merupakan diagonal bidang adalah titik A ke C sedangkan diagonal ruang adalah titik C ke H

Diagonal Bidang

Seperti penjelasan saya sebelumnya bahwa diagonal bidang itu sama dengan diagonal sisi yaitu garis yang menghubungkan antara dua titik sudut yang berhadapan pada setiap bidang atau sisi kubus. lihat gambar

Diagonal bidang kubus dari gambar diatas adalah AC, AE, AG, BD, BF, BH, CE, CG, DF, DH, EG, FH

sehingga kubus memiliki diagonal bidang sebanyak = 12 Buah

Rumus Diagonal Bidang Kubus

Rumus baku dari diagonal bidang kubus adalah S√2 . S adalah SISI

mencari rumusnya adalah menggunakan teorema phytagoras. namun karena bentuk dari persegi itu sisinya sama maka rumus paling singkatnya sudah diketahui. namun jika kamu ingin mengetahuinya lebih detail bisa cek. 

Coba lihat kembali gambar diatas :

Untuk Menghitung titik AC (diagonal ruang) maka diperlukan rumus sebagai berikut:

AC² = AB² + BC²

AC = √AB + BC

AC = S√2

Jangan bingung ya. AB dan BC itu sama dengan S (sisi). lihat contoh soal

Diagonal Ruang Kubus

Diagonal ruang merupakan garis yang membentang dari suatu titik ke titik lainnya dengan melewati bagian tengah. lihat contoh gambar

Garis antara titik H ke titik C disebut dengan diagonal ruang. sehingga dapat disimpulkan bahwa :

• Diagonal ruang gambar diatas adalah titik = AF, BE, DG, HC, 
• Jumlah Diagonal ruang kubus = 4

Rumus Diagonal Ruang

Rumus baku dari diagonal ruang adalah S√3. rumus tersebut di dapatkan dari perhitungan cukup panjang menggunakan teorema phytagoras

Kalau mau membuktikan bisa lihat contoh soal berikut ini. terutama nomor 2

Contoh Soal Diagonal Ruang dan Bidang

1. Hitunglah diagonal ruang dan diagonal bidang kubus yang memiliki panjang sisi 5 cm?

Jawaban:

Diagonal Bidang = S√2= 5√2 cm

Diagonal Ruang = S√3 = 5√3 cm

2. 

Hitunglah Diagonal ruang dan diagonal bidang gambar diatas?

Jawaban

Diagonal Bidang

= S√2

= 10√2 cm

Diagonal Ruang

= S√3

= 10√3 cm

untuk membuktikannya mari kita coba hitung dengan rumus yang agak panjang. ini masih menjawab soal nomor 2 ya

Diagonal bidang?

diagonal bidang sama dengan AC

AC² = AB² + BC²

AC² = 10² + 10²

AC² = 100 + 100

AC = √200

AC = √100 x √2

AC = 10√2 cm

Diagonal Ruang?

diagonal ruang sama dengan AF. karena AC sudah kita hitung maka sekarang kita hanya perlu mengitung AF saja

AF² = AC²+AF²

AF² = (10√2)² + 10²

AF = √200 + √100

AF = √300

AF = √100 x √3

AF = 10 √3 cm

Mau pakai cara instan atau cara yang njelimet silahkan. yang penting kamu harus faham mengenai diagonal ruang dan diagonal sisi mulai dari jumlah hingga rumus. selamat belajar